悬线法

原理

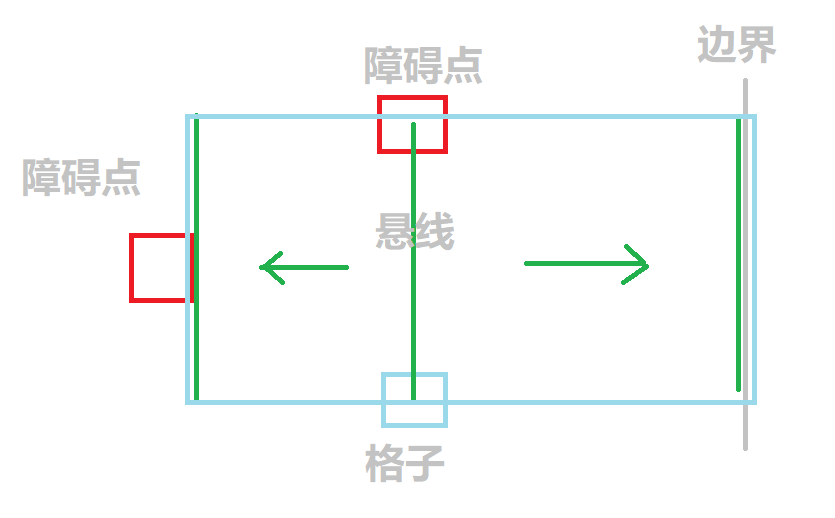
up[i][j]记录格子(i, j)的悬线长度。

left[i][j]记录格子(i, j)的悬线向左扩展到的位置。

right[i][j]记录格子(i, j)的悬线向右扩展到的位置。

模板题

洛谷-P4147-玉蟾宫

#include <iostream>
#define left LeFt
#define right RiGhT
using namespace std;

const int N = 1010;
char a[N][N];
int up[N][N], left[N][N], right[N][N];

int main () {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            cin >> a[i][j];
            up[i][j] = 1;
            left[i][j] = right[i][j] = j;
        }
    }

    for (int i = 1; i <= n; ++ i) // 预处理left
        for (int j = 2; j <= m; ++ j)
            if (a[i][j] == a[i][j - 1] && a[i][j] == 'F')
                left[i][j] = left[i][j - 1];

    for (int i = 1; i <= n; ++ i) // 预处理right
        for (int j = m - 1; j >= 1; -- j)
            if (a[i][j] == a[i][j + 1] && a[i][j] == 'F')
                right[i][j] = right[i][j + 1];

    int res = 0;
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            if (i >= 2
                && a[i][j] == a[i - 1][j]
                && a[i - 1][j] == 'F'
            ) {
                up[i][j] = up[i - 1][j] + 1;
                left[i][j] = max(left[i][j], left[i - 1][j]);
                right[i][j] = min(right[i][j], right[i - 1][j]);
            }
            if (a[i][j] == 'F')
                res = max(res, up[i][j] * (right[i][j] - left[i][j] + 1));
        }
    }
    cout << res * 3 << endl;
    return 0;
}