ST表

原理

见《进阶指南》第41页。

预处理

$f[i][j]$记录从$a[i]$到a[i+2​j​​−1]共2​j​​个数的最大值。

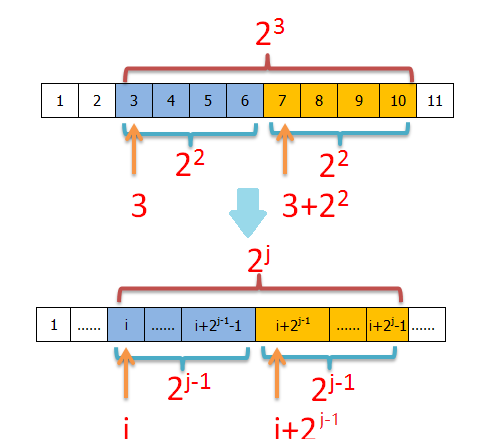
状态转移方程：f[i][j]=max(f[i][j−1],f[i+2​j−1​​][j−1])。

两个上界：

• 由2​j​​≤n得，j≤log​2​​(n)。

• 由i+2​j​​−1≤n得， i≤n−2​j​​+1。

查询

下文以len表示待查询区间的长度。

设k=⌊log​2​​(len)⌋。

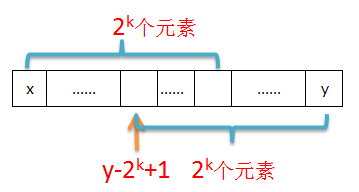
• 当待查询区间的长度是2的非负整数次幂时，2×2​k​​=2×2​⌊log​2​​(len)⌋​​=2×len>len。

• 当待查询区间的长度不是2的非负整数次幂时，2×2​k​​=2×2​⌊log​2​​(len)⌋​​=2​⌊log​2​​(len)⌋+1​​=2​⌈log​2​​(len)⌉​​>len。

时间复杂度

预处理：$O(nlogn)$。

查询：$O(1)$。

模板题

洛谷-P3865-【模板】ST表

#include <iostream>
#include <cmath>
using namespace std;

const int N = 100010;
int n, q;
int a[N], f[N][20];

void ST_create () {
    for (int i = 1; i <= n; ++ i) f[i][0] = a[i];
    int k = log(n) / log(2);
    for (int j = 1; j <= k; ++ j)
        for (int i = 1; i <= n - (1 << j) + 1; ++ i)
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
int ST_query (int l, int r) {
    int k = log(r - l + 1) / log(2);
    return max(f[l][k], f[r - (1 << k) + 1][k]);
}

int main () {
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);

    ST_create();
    while (q --) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", ST_query(l, r));
    }
    return 0;
}