`cdq`分治

原理

见《进阶指南》第244页。
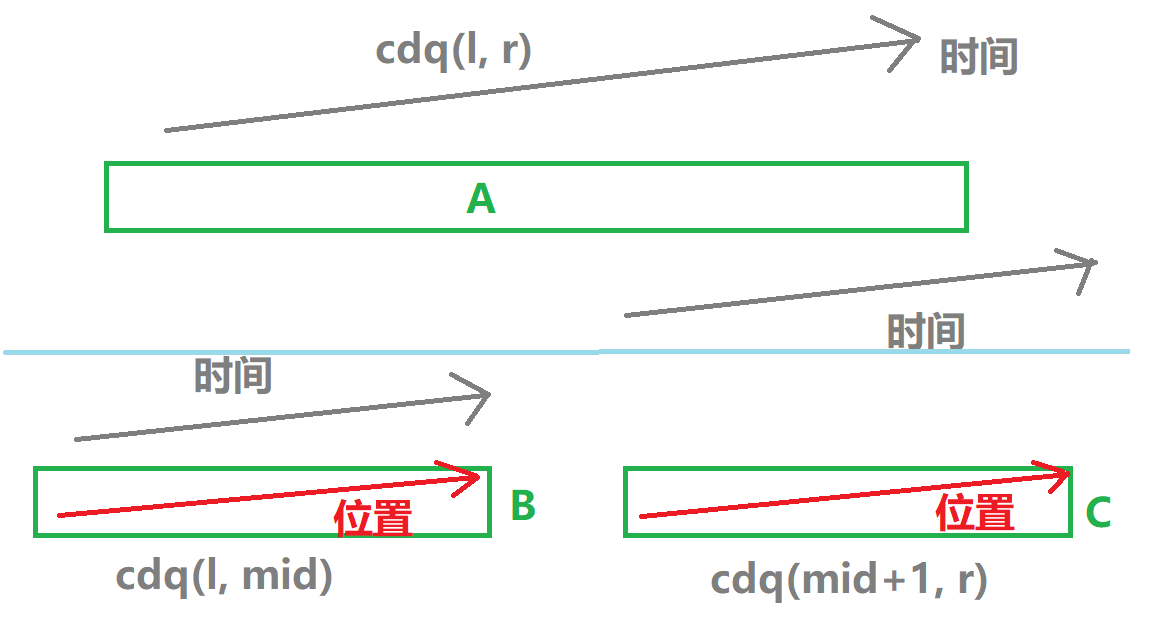
每一次修改会对时间较后且下标不较前的查询产生影响。
模板题

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 500010;
struct operation {
    int type; // 操作的类型，1：修改，2、3：查询
    int idx;
    LL val;
    bool operator < (const operation& o) const {
        if (idx == o.idx)
            return type < o.type;
        return idx < o.idx;
    }
};
operation a[3 * N], temp[3 * N];
LL res[N];

void cdq (int l, int r) {
    if (l >= r) return;

    int mid = l + r >> 1;
    cdq(l, mid);
    cdq(mid + 1, r);

    int i = l, j = mid + 1, k = l;
    LL sum = 0;
    while (i <= mid && j <= r) { // 左 -> 右
        if (a[i] < a[j]) {
            if (a[i].type == 1)
                sum += a[i].val;
            temp[k ++] = a[i ++];
        } else {
            if (a[j].type == 2)
                res[a[j].val] -= sum;
            if (a[j].type == 3)
                res[a[j].val] += sum;
            temp[k ++] = a[j ++];
        }
    }
    while (i <= mid) temp[k ++] = a[i ++];
    while (j <= r) {
        if (a[j].type == 2)
            res[a[j].val] -= sum;
        if (a[j].type == 3)
            res[a[j].val] += sum;
        temp[k ++] = a[j ++];
    }
    for (int i = l; i <= r; ++ i) a[i] = temp[i];
}

int main () {
    int n, m, idx = 0, cnt = 0; // 第 cnt 次查询
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) {
        a[++ idx].type = 1; // 修改
        a[idx].idx = i;
        scanf("%lld", &a[idx].val);
    }
    for (int i = 1, opt; i <= m; ++ i) {
        scanf("%d", &opt);
        if (opt == 1) {
            a[++ idx].type = 1;
            scanf("%d%lld", &a[idx].idx, &a[idx].val);
        } else {
            int l, r;
            scanf("%d%d", &l, &r);
            a[++ idx] = { 2, l - 1, ++ cnt};
            a[++ idx] = { 3, r, cnt };
        }
    }
    // 此时，操作序列 a 在时间上是有序（升序）的
    cdq(1, idx);
    for (int i = 1; i <= cnt; ++ i)
        printf("%lld\n", res[i]);
    return 0;
}
# cdq分治

# 原理

# 模板题

`cdq`分治

原理

模板题
