分层图最短路

原理

k + 1个层次，k个层间。

对于有向边u -> v，对于顶点u，除了要向本层的顶点v连一条权值为w的有向边，还要向下一层的顶点v连一条权值为0的有向边。

从本层的顶点移动到下一层的顶点相当于一次免费搭乘。

航线不足k条的情况：

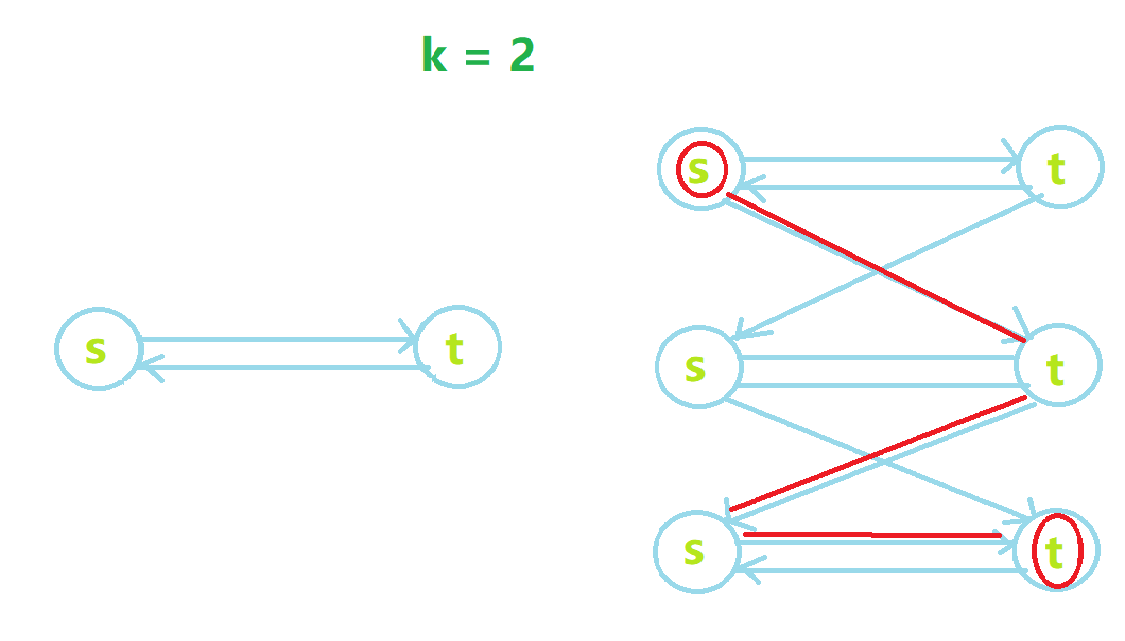
解决方法：本层的终点t向下一层的终点t连一条权值为0的有向边，以消耗掉多余的免费搭乘机会。

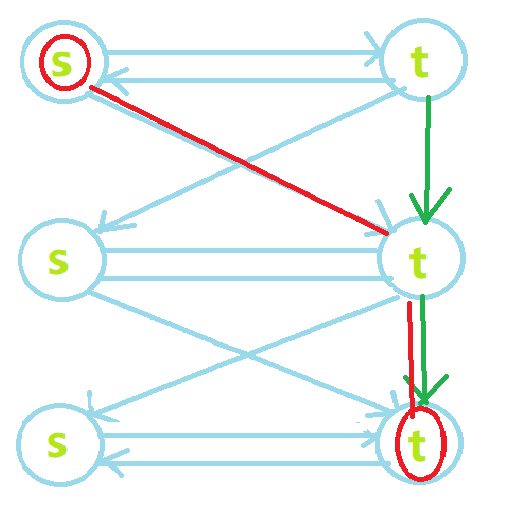
模板题

洛谷-P4568-飞行路线

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N = 110010, M = 2100010; // (k + 1) * 10w + k * 10w
struct edge {
    int to, next, w;
};
edge e[M];
int idx, head[N];
struct node {
    int idx, dis;
    bool operator < (const node& o) const {
        return dis > o.dis;
    }
};
int n, m, k, s, t;
int dis[N];
bool mark[N];

void add_edge (int u, int v, int w) {
    e[idx].w = w;
    e[idx].to = v;
    e[idx].next = head[u];
    head[u] = idx ++;
}
void dijkstra () {
    memset(dis, 0x3f, sizeof(dis));

    priority_queue<node> pq;
    dis[s] = 0;
    pq.push({ s, dis[s] });
    while (!pq.empty()) {
        int cur = pq.top().idx;
        pq.pop();
        if (mark[cur] == true) continue;
        mark[cur] = true;
        for (int i = head[cur]; i != -1; i = e[i].next) {
            int to = e[i].to, w = e[i].w;
            if (dis[cur] + w < dis[to]) {
                dis[to] = dis[cur] + w;
                pq.push({ to, dis[to] });
            }
        }
    }
}

int main () {
    memset(head, -1, sizeof(head));
    cin >> n >> m >> k >> s >> t;
    for (int i = 1, u, v, w; i <= m; ++ i) {
        cin >> u >> v >> w;
        add_edge(u, v, w);
        add_edge(v, u, w);
        for (int j = 1; j <= k; ++ j) {
            add_edge(u + (j - 1) * n, v + j * n, 0);
            add_edge(v + (j - 1) * n, u + j * n, 0);

            add_edge(u + j * n, v + j * n, w);
            add_edge(v + j * n, u + j * n, w);
        }
    }
    for (int j = 1; j <= k; ++ j) // 航线可能不足 k 条
        add_edge(t + (j - 1) * n, t + j * n, 0);
    dijkstra();
    cout << dis[t + k * n] << endl;
    return 0;
}