最大流

原理

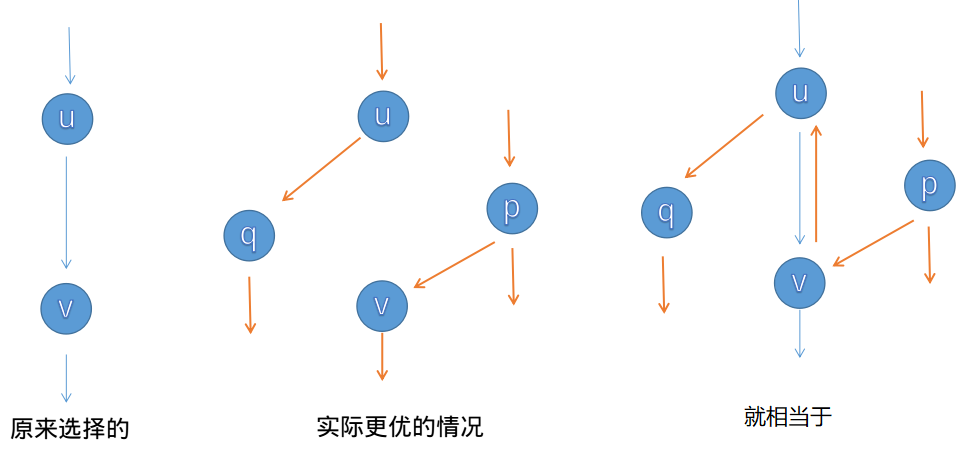
见《进阶指南》第441页。

Dinic算法。

模板题

AcWing-2172-Dinic/ISAP求最大流

#include <iostream>
#include <cstring>
#include <queue>
#define inf 0x3f3f3f3f
using namespace std;

const int N = 10010, M = 100010;
struct edge {
    int to, next, w; // 剩余容量
};
edge e[2 * M];
int idx, head[N];
int n, m, S, T;
int d[N], arc[N];

void add_edge (int u, int v, int w) {
    e[idx].w = w;
    e[idx].to = v;
    e[idx].next = head[u];
    head[u] = idx ++;

    e[idx].w = 0;
    e[idx].to = u;
    e[idx].next = head[v];
    head[v] = idx ++;
}
bool bfs () { // 在残量网络上构造分层图
    memset(d, 0, sizeof(d));
    d[S] = 1;
    arc[S] = head[S];
    queue<int> q;
    q.push(S);
    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        for (int i = head[cur]; i != -1; i = e[i].next) {
            int to = e[i].to, w = e[i].w;
            if (d[to] == 0 && w) {
                d[to] = d[cur] + 1;
                arc[to] = head[to];
                q.push(to);
                if (to == T) return true;
            }
        }
    }
    return false;
}
int dinic (int cur, int flow) { // 在当前分层图上增广
    if (cur == T) return flow;

    int rest = flow;
    for (int i = arc[cur]; i != -1 && rest; i = e[i].next) {
        int to = e[i].to, w = e[i].w;
        arc[cur] = i; // 当前弧优化（避免重复遍历从 cur 出发不可扩展的边）
        if (d[to] == d[cur] + 1 && w) {
            int k = dinic(to, min(rest, w));
            if (k == 0) d[to] = 0; // 剪枝，去掉增广完毕的点
            e[i].w -= k;
            e[i ^ 1].w += k;
            rest -= k;
        }
    }
    return flow - rest;
}

int main () {
    memset(head, -1, sizeof(head));
    scanf("%d%d%d%d", &n, &m, &S, &T);
    for (int i = 1, u, v, w; i <= m; ++ i) {
        scanf("%d%d%d", &u, &v, &w);
        add_edge(u, v, w);
    }

    int max_flow = 0, flow;
    while (bfs() == true)
        while (flow = dinic(S, inf))
            max_flow += flow;
    printf("%d", max_flow);
    return 0;
}