权值线段树合并

原理

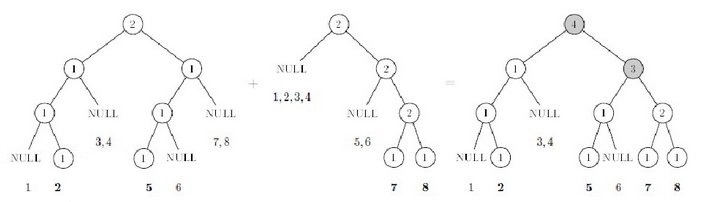
见《进阶指南》第223页。

模板题

洛谷-P4556-雨天的尾巴 /【模板】线段树合并

#include <iostream>
#include <cstring>
#include <algorithm>
#define size SiZe
#define null 0
using namespace std;

const int N = 100010;
struct edge {
    int to, next;
};
edge e[2 * N];
int idx, head[N];
int n, m;
struct node {
    int x, y, z;
};
node rec[N];
int cnt, nums[N];
int dep[N], fa[N], size[N];
int heavy_son[N], top[N];
struct segmentTreeNode {
    int ls, rs;
    int data, pos;
    #define ls(x) t[x].ls
    #define rs(x) t[x].rs
    #define data(x) t[x].data
    #define pos(x) t[x].pos
};
segmentTreeNode t[N * 4 * 20];
int tot, root[N];

void discrete () {
    for (int i = 1; i <= m; ++ i) nums[i] = rec[i].z;
    sort(nums + 1, nums + m + 1);
    cnt = unique(nums + 1, nums + m + 1) - (nums + 1);
    for (int i = 1; i <= m; ++ i)
        rec[i].z = lower_bound(nums + 1, nums + cnt + 1, rec[i].z) - nums;
}
void add_edge (int u, int v) {
    e[idx].to = v;
    e[idx].next = head[u];
    head[u] = idx ++;
}
void dfs1 (int cur, int father) {
    size[cur] = 1;
    for (int i = head[cur]; i != -1; i = e[i].next) {
        int to = e[i].to;
        if (to == father) continue;
        dep[to] = dep[cur] + 1;
        fa[to] = cur;
        dfs1(to, cur);
        size[cur] += size[to];
        if (size[to] > size[heavy_son[cur]])
            heavy_son[cur] = to;
    }
}
void dfs2 (int cur, int top_node) {
    top[cur] = top_node;
    if (heavy_son[cur]) dfs2(heavy_son[cur], top_node);
    for (int i = head[cur]; i != -1; i = e[i].next) {
        int to = e[i].to;
        if (to == fa[cur] || to == heavy_son[cur]) continue;
        dfs2(to, to);
    }
}
int lca (int x, int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    return x;
}
void update (int rt) {
    data(rt) = max(data(ls(rt)), data(rs(rt)));
    pos(rt) = data(ls(rt)) >= data(rs(rt)) ? pos(ls(rt)) : pos(rs(rt));
}
int modify (int rt, int l, int r, int val, int delta) {
    if (rt == null) rt = ++ tot;
    if (l == r) {
        data(rt) += delta;
        pos(rt) = data(rt) >= 1 ? l : 0;
        return rt;
    }
    int mid = l + r >> 1;
    if (val <= mid)
        ls(rt) = modify(ls(rt), l, mid, val, delta);
    else
        rs(rt) = modify(rs(rt), mid + 1, r, val, delta);
    update(rt);
    return rt;
}
int merge (int x, int y, int l, int r) {
    if (x == null || y == null) return x + y;
    if (l == r) {
        data(x) += data(y);
        pos(x) = data(x) >= 1 ? l : 0;
        return x;
    }
    int mid = l + r >> 1;
    ls(x) = merge(ls(x), ls(y), l, mid);
    rs(x) = merge(rs(x), rs(y), mid + 1, r);
    update(x);
    return x;
}
void dfs3 (int cur, int father) {
    for (int i = head[cur]; i != -1; i = e[i].next) {
        int to = e[i].to;
        if (to == father) continue;
        dfs3(to, cur);
        root[cur] = merge(root[cur], root[to], 1, cnt);
    }
}

int main () {
    memset(head, -1, sizeof(head));
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= n - 1; ++ i) {
        scanf("%d%d", &u, &v);
        add_edge(u, v);
        add_edge(v, u);
    }
    for (int i = 1; i <= m; ++ i)
        scanf("%d%d%d", &rec[i].x, &rec[i].y, &rec[i].z);

    discrete();
    dfs1(1, -1);
    dfs2(1, 1);
    for (int i = 1; i <= n; ++ i) root[i] = ++ tot;
    for (int i = 1; i <= m; ++ i) {
        int x = rec[i].x, y = rec[i].y, z = rec[i].z;
        int t = lca(x, y);
        root[x] = modify(root[x], 1, cnt, z, 1);
        root[y] = modify(root[y], 1, cnt, z, 1);
        root[t] = modify(root[t], 1, cnt, z, -1);
        if (fa[t])
            root[fa[t]] = modify(root[fa[t]], 1, cnt, z, -1);
    }
    dfs3(1, -1);
    for (int i = 1; i <= n; ++ i)
        printf("%d\n", nums[pos(root[i])]);
    return 0;
}