多重背包

直接拆分法

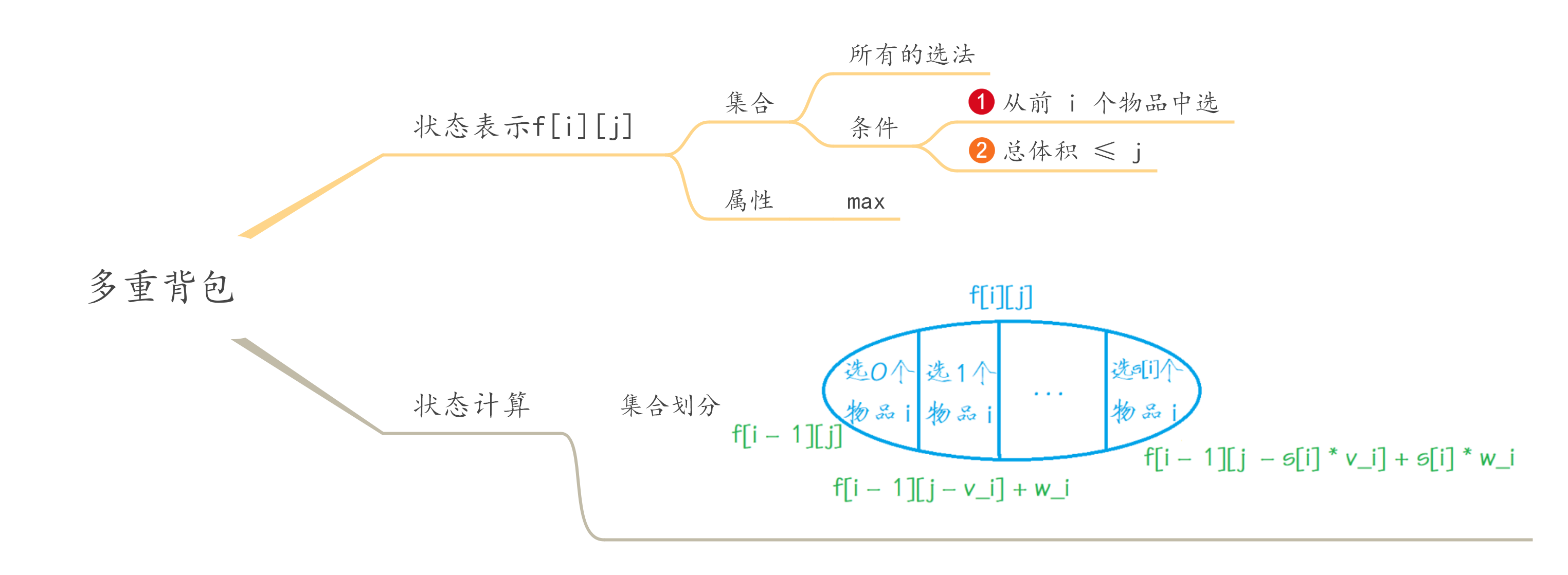
原理

见《进阶指南》第279页。

模板题

AcWing-4-多重背包问题 I

#include <iostream>
using namespace std;

const int N = 110;
struct node {
    int v, w, s;
};
int n, m;
node a[N];
int f[N][N];

int main () {
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> a[i].v >> a[i].w >> a[i].s;

    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j <= m; ++ j)
            for (int k = 0; k <= min(a[i].s, j / a[i].v); ++ k)
                f[i][j] = max(f[i][j], f[i - 1][j - k * a[i].v] + k * a[i].w);
    cout << f[n][m] << endl;
    return 0;
}

二进制拆分法

原理

见《进阶指南》第280页。

模板题

AcWing-4-多重背包问题 II

#include <iostream>
using namespace std;

const int N = 12000; // log_2(2000) ≈ 11
struct node {
    int v, w;
};
int n, m, idx;
node a[N];
int f[N];

int main () {
    cin >> n >> m;
    for (int i = 1, v, w, s; i <= n; ++ i) {
        cin >> v >> w >> s;
        int p = 1;
        while (p <= s) {
            a[++ idx] = { p * v, p * w };
            s -= p;
            p *= 2;
        }
        if (s > 0) a[++ idx] = { s * v, s * w };
    }
    for (int i = 1; i <= idx; ++ i)
        for (int j = m; j >= a[i].v; -- j)
            f[j] = max(f[j], f[j - a[i].v] + a[i].w);
    cout << f[m] << endl;
    return 0;
}

单调队列优化

原理

见《进阶指南》第280页。

模板题

AcWing-6-多重背包问题 III

#include <iostream>
#include <queue>
using namespace std;

const int N = 1010, M = 20010;
struct node {
    int v, w, s;
};
int n, m;
node a[N];
deque<int> dq;
int f[M];

int cal (int i, int r, int k) {
    return f[k * a[i].v + r] - k * a[i].w;
}

int main () {
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> a[i].v >> a[i].w >> a[i].s;

    for (int i = 1; i <= n; ++ i) {
        int v = a[i].v, w = a[i].w, s = a[i].s;
        for (int r = 0; r <= v - 1; ++ r) {
            int max_p = (m - r) / v;
            for (int k = max_p - 1; k >= max(max_p - s, 0); -- k) {
                while (!dq.empty() && cal(i, r, dq.back()) <= cal (i, r, k))
                    dq.pop_back();
                dq.push_back(k);
            }
            for (int p = max_p; p >= 0; -- p) {
                if (!dq.empty() && dq.front() > p - 1) dq.pop_front();
                if (!dq.empty())
                    f[p * v + r] = max(f[p * v + r], cal(i, r, dq.front()) + p * w);
                if (p - s - 1 >= 0) {
                    while (!dq.empty() && cal(i, r, dq.back()) <= cal(i, r, p - s - 1))
                        dq.pop_back();
                    dq.push_back(p - s - 1);
                }
            }
        }
    }
    int res = 0;
    for (int i = 1; i <= m; ++ i)
        res = max(res, f[i]);
    cout << res << endl;
    return 0;
}