动态中位数

AcWing-106-动态中位数

分析

见《进阶指南》第36页。

对顶堆：

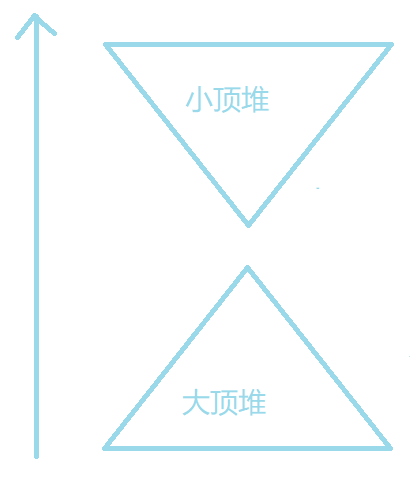
将大顶堆中所有元素组成的集合记为A，小顶堆中所有元素组成的集合记为B。

大顶堆的堆顶元素是集合A中元素的最大值，记为max；小顶堆的堆顶元素是集合B中元素的最小值，记为min。

显然有min ≥ max，即集合B中的任意一个元素大于等于集合A中的任意一个元素。

将集合A与集合B的并集记为U。

若集合A的大小为n，集合B的大小为m，则集合A的元素为集合U的前n小，集合B的元素为集合U的前m大。

因为min是前m大中最小的，所以min是第m大；同理max是第n小。

如果大顶堆的大小比小顶堆大1，那么大顶堆的堆顶元素就是集合U的中位数。

如果小顶堆的大小比大顶堆大1，那么小顶堆的堆顶元素就是集合U的中位数。

实现

#include <iostream>
#include <queue>
using namespace std;

int main () {
    int T;
    scanf("%d", &T);
    while (T --) {
        priority_queue<int> max_heap;
        priority_queue<int, vector<int>, greater<int> > min_heap;

        int idx, n;
        scanf("%d%d", &idx, &n);
        printf("%d %d\n", idx, n / 2 + 1);

        int cnt = 0;
        for (int i = 1, val; i <= n; ++ i) {
            scanf("%d", &val);
            if (i % 2 == 1) {
                min_heap.push(val);
                while (!max_heap.empty()
                    && max_heap.top() > min_heap.top()
                ) {
                    int a = max_heap.top();
                    max_heap.pop();
                    int b = min_heap.top();
                    min_heap.pop();

                    max_heap.push(b);
                    min_heap.push(a);
                }
                printf("%d ", min_heap.top());
                if ((++ cnt) % 10 == 0) printf("\n");
            } else {
                max_heap.push(val);
            }
        }
        if (cnt % 10 != 0) printf("\n");
    }
    return 0;
}