Legacy

洛谷-CF786B-Legacy

分析

线段树优化建图。

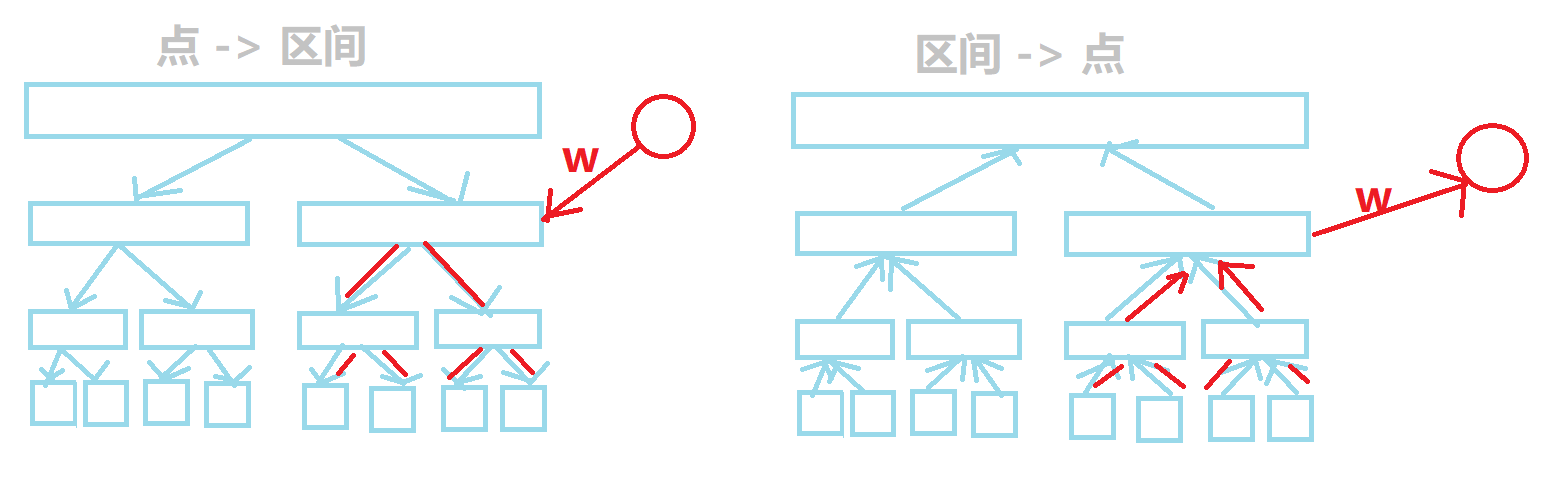
实现

#include <iostream>
#include <cstring>
#include <queue>
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;

typedef long long LL;
const int N = 800010, M = 2000010;
struct edge {
    int to, next, w;
};
edge e[M];
int idx, head[N];
int n, m, s;
struct node {
    int ls, rs;
    #define ls(x) t[x].ls
    #define rs(x) t[x].rs
};
int tot, root[3];
node t[N];
LL dis[N];
bool mark[N];

void add_edge (int u, int v, int w) {
    e[idx].w = w;
    e[idx].to = v;
    e[idx].next = head[u];
    head[u] = idx ++;
}
int build1 (int l, int r) {
    if (l == r) return l; // 1 ~ n

    int cur = ++ tot;
    int mid = l + r >> 1;
    ls(cur) = build1(l, mid);
    rs(cur) = build1(mid + 1, r);
    // 父 -> 子
    add_edge(cur, ls(cur), 0);
    add_edge(cur, rs(cur), 0);
    return cur;
}
// u -> [a, b]
void modify1 (int rt, int l, int r, int u, int a, int b, int w) {
    if (a <= l && r <= b) {
        add_edge(u, rt, w);
        return;
    }

    int mid = l + r >> 1;
    if (a <= mid) modify1(ls(rt), l, mid, u, a, b, w);
    if (b >= mid + 1) modify1(rs(rt), mid + 1, r, u, a, b, w);
}
int build2 (int l, int r) {
    if (l == r) return l; // 1 ~ n

    int cur = ++ tot;
    int mid = l + r >> 1;
    ls(cur) = build2(l, mid);
    rs(cur) = build2(mid + 1, r);
    // 子 -> 父
    add_edge(ls(cur), cur, 0);
    add_edge(rs(cur), cur, 0);
    return cur;
}
// [a, b] -> v
void modify2 (int rt, int l, int r, int a, int b, int v, int w) {
    if (a <= l && r <= b) {
        add_edge(rt, v, w);
        return;
    }

    int mid = l + r >> 1;
    if (a <= mid) modify2(ls(rt), l, mid, a, b, v, w);
    if (b >= mid + 1) modify2(rs(rt), mid + 1, r, a, b, v, w);
}
void spfa (int s) {
    memset(dis, 0x3f, sizeof(dis));

    queue<int> q;
    dis[s] = 0;
    q.push(s);
    mark[s] = true;
    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        mark[cur] = false;
        for (int i = head[cur]; i != -1; i = e[i].next) {
            int to = e[i].to, w = e[i].w;
            if (dis[cur] + w < dis[to]) {
                dis[to] = dis[cur] + w;
                if (mark[to] == false) {
                    q.push(to);
                    mark[to] = true;
                }
            }
        }
    }
}

int main () {
    memset(head, -1, sizeof(head));
    cin >> n >> m >> s;

    tot = n; // 线段树结点的编号从 n + 1 开始
    root[1] = build1(1, n);
    root[2] = build2(1, n);
    for (int i = 1, opt; i <= m; ++ i) {
        cin >> opt;
        if (opt == 1) { // 点 -> 点
            int u, v, w;
            cin >> u >> v >> w;
            add_edge(u, v, w);
        } else if (opt == 2) { // 点 -> 区间
            int u, l, r, w;
            cin >> u >> l >> r >> w;
            modify1(root[1], 1, n, u, l, r, w);
        } else { // 区间 -> 点
            int v, l, r, w;
            cin >> v >> l >> r >> w;
            modify2(root[2], 1, n, l, r, v, w);
        }
    }
    spfa(s);
    for (int i = 1; i <= n; ++ i)
        cout << (dis[i] == inf ? -1 : dis[i]) << ' ';
    return 0;
}