饼干

AcWing-277-饼干

分析

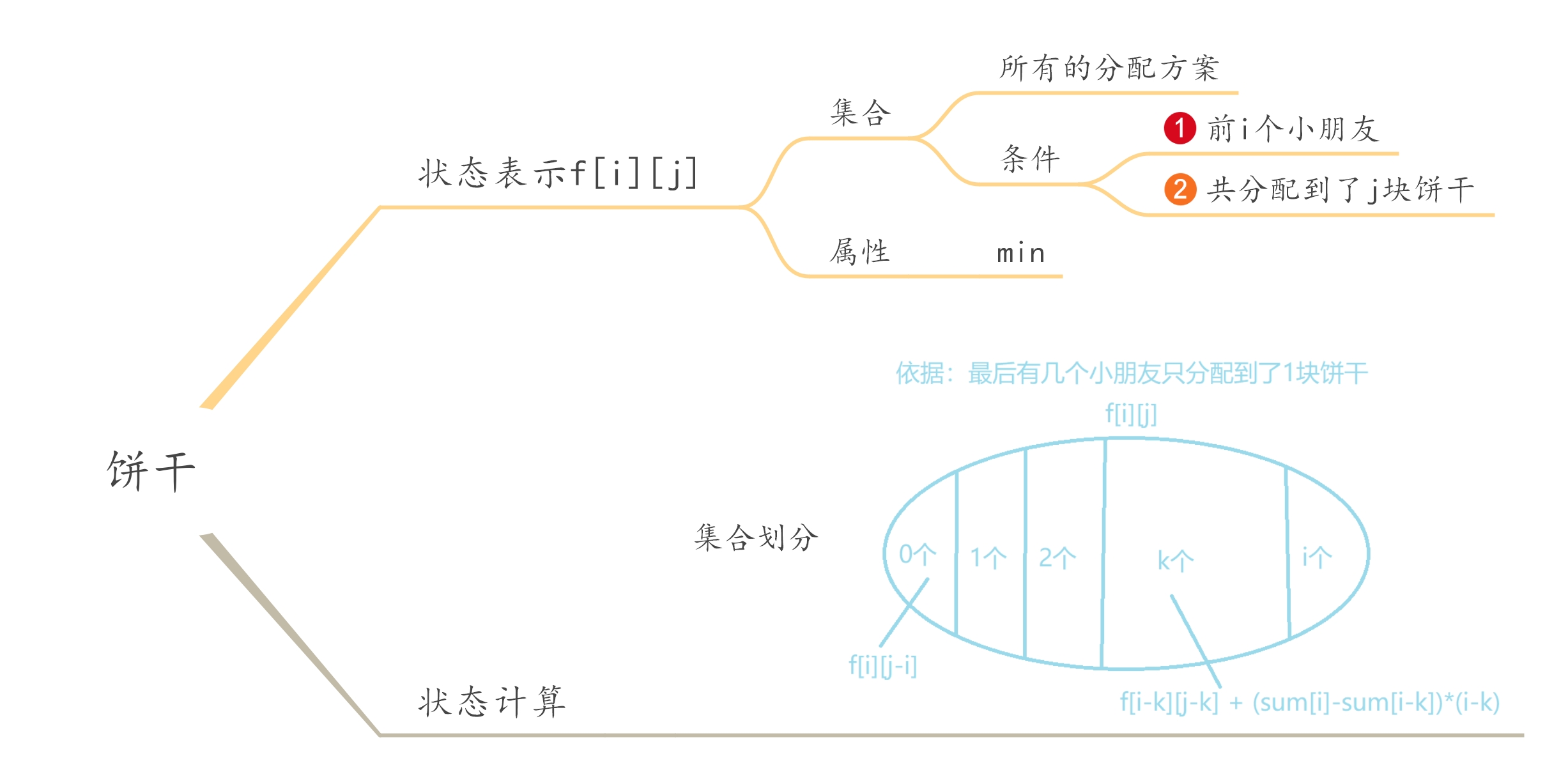
见《进阶指南》第273页。

实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 32, M = 5010;
struct node {
    int val, idx;
    bool operator < (const node& o) const {
        return val > o.val;
    }
};
int n, m;
node g[N];
int sum[N];
int f[N][M];
int res[M];

int main () {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i) {
        scanf("%d", &g[i].val);
        g[i].idx = i;
    }

    sort(g + 1, g + n + 1);
    for (int i = 1; i <= n; ++ i) sum[i] = sum[i - 1] + g[i].val;
    memset(f, 0x3f, sizeof(f));
    f[0][0] = 0;
    for (int i = 1; i <= n; ++ i) {
        for (int j = i; j <= m; ++ j) {
            f[i][j] = f[i][j - i];
            for (int k = 1; k <= i; ++ k)
                f[i][j] = min(f[i][j], f[i - k][j - k] + (sum[i] - sum[i - k]) * (i - k));
        }
    }
    printf("%d\n", f[n][m]);

    int i = n, j = m, h = 0;
    while (i >= 1) {
        if (f[i][j] == f[i][j - i]) {
            j -= i;
            ++ h;
        } else {
            for (int k = 1; k <= i; ++ k) {
                if (f[i][j] == f[i - k][j - k] + (sum[i] - sum[i - k]) * (i - k)) {
                    for (int u = i - k + 1; u <= i; ++ u)
                        res[g[u].idx] = h + 1;
                    i -= k;
                    j -= k;
                    break;
                }
            }
        }
    }
    for (int i = 1; i <= n; ++ i)
        printf("%d ", res[i]);
    return 0;
}